STRENGTH OF MATERIALS || CHAPTER 01 || TANGENTIAL STRESS AND LONGITUDINAL STRESS
Thin-Walled Pressure Vessels
A tank or pipe carrying a fluid or gas under a pressure is subjected to tensile forces, which resist bursting, developed across longitudinal and transverse sections.
TANGENTIAL STRESS : (Circumferential Stress)
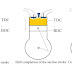
Consider the tank shown being subjected to an internal pressure p. The length of the tank is L and the wall thickness is t. Isolating the right half of the tank:
If there exist an external pressure Po and an internal pressure Pi, the formula may be expressed as:
LONGITUDINAL STRESS, σL
Consider the free body diagram in the transverse section of the tank:
The total force acting at the rear of the tank F must equal to the total longitudinal stress
on the wall PT = σL A(wall). Since t is so small compared to D, the area of the wall is close to πDt
If there exist an external pressure po and an internal pressure pi, the formula may be expressed as:
It can be observed that the tangential stress is twice that of the longitudinal stress.
σt = 2 σ L
SPHERICAL SHELL
If a spherical tank of diameter D and thickness t contains gas under a pressure of p, the stress at the wall can be expressed as:
Problem 133
A cylindrical steel pressure vessel 400 mm in diameter with a wall thickness of 20 mm, is subjected to an internal pressure of 4.5 MN/m2.
(a) Calculate the tangential and longitudinal stresses in the steel.
(b) To what value may the internal pressure be increased if the stress in the steel is limited to 120 MN/m2?
(c) If the internal pressure were increased until the vessel burst, sketch the type of fracture that would occur.

Problem 134
The wall thickness of a 4-ft-diameter spherical tank is 5/16 inch. Calculate the allowable internal pressure if the stress is limited to 8000 psi.
Solution :
Problem 135
Calculate the minimum wall thickness for a cylindrical vessel that is to carry a gas at a pressure of 1400 psi. The diameter of the vessel is 2 ft, and the stress is limited to 12 ksi.
Solution :
Problem 136
A cylindrical pressure vessel is fabricated from steel plating that has a thickness of 20 mm. The diameter of the pressure vessel is 450 mm and its length is 2.0 m. Determine the maximum internal pressure that can be applied if the longitudinal stress is limited to 140 MPa, and the circumferential stress is limited to 60 MPa.
Solution:
Problem 137
A water tank, 22 ft in diameter, is made from steel plates that are 1/2 in. thick. Find the maximum height to which the tank may be filled if the circumferential stress is limited to 6000 psi. The specific weight of water is 62.4 lb/ft3.
Solution:
Problem 138
The strength of longitudinal joint in Fig. 1-17 is 33 kips/ft, whereas for the girth is 16 kips/ft. Calculate the maximum diameter of the cylinder tank if the internal pressure is
150 psi.
Solution:
Problem 139
Find the limiting peripheral velocity of a rotating steel ring if the allowable stress is 20 ksi and steel weighs 490 lb/ft3. At what revolutions per minute (rpm) will the stress reach 30 ksi if the mean radius is 10 in.?
Solution:
Problem 140
At what angular velocity will the stress of t he rotating steel ring equal 150 MPa if its mean radius is 220 mm? The density of steel 7.85 Mg/m3.
Solution:
Problem 141
The tank shown in Fig. P-141 is fabricated from 1/8-in steel plate. Calculate the
maximum longitudinal and circumferential stress caused by an internal pressure of 125 psi.
Solution:
Problem 142
A pipe carrying steam at 3.5 MPa has an outside diameter of 450 mm and a wall
thickness of 10 mm. A gasket is inserted between the flange at one end of the pipe and a flat plate used to cap the end. How many 4 0-mm-diameter bolts must be used to hold the cap on if the allowable stress in the bolts is 80 MPa, of which 55 MPa is the initial stress? What circumferential stress is developed in the pipe? Why is it necessary to tighten the bolt initially, and what will happen if the steam pressure should cause the stress in the bolts to be twice the value of the initial stress?
Solution:



































No comments